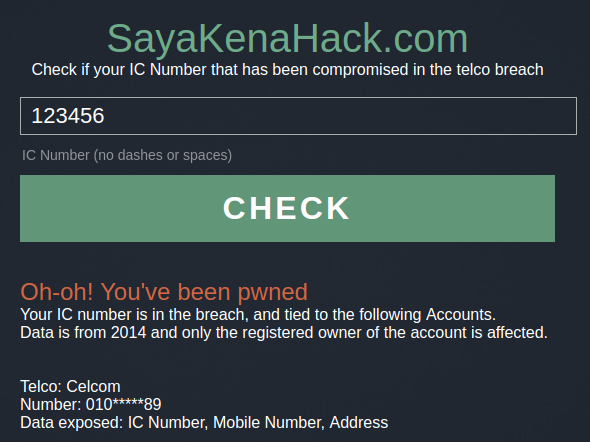
Why does SayaKenaHack have dummy data?

Why does sayakenahack have dummy data? If I enter “123456” and “112233445566” I still get results.

I was struggling with answering this question, as some folks have used it to ‘prove’ that I was a phisher. We’ll get to that later, for now I hope to answer why these ‘fake’ IC numbers exist in the sayakenahack.

Firstly, I couldn’t find a good enough way to validate IC numbers as I was inserting them into the database. Most of you think that IC numbers follow a pre-define pattern :

• 6-digit birthday (yymmdd format)
• 2-digit state code
• 4-digit personal identifier, where the last digit is odd for men, and even for women.

But, there are still folks with old IC numbers, and the army have their own format. Not to mention that the IC Number field  can be populated by passport numbers (for foreigners) and Company registration IDs. So instead of cracking my head on how to validate IC numbers, I decided to pass them all in.

The only ‘transformation’ I do is to strip them of all non-AlphaNumeric characters and uppercasing any letters in the result. This would standardize the IC numbers in the database, regardless of source file format.

Had I done some validation, I might have removed these dummy entries — but fortunately I didn’t.

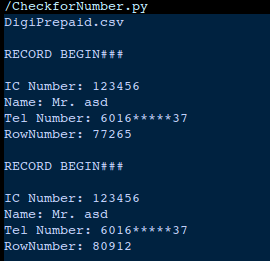
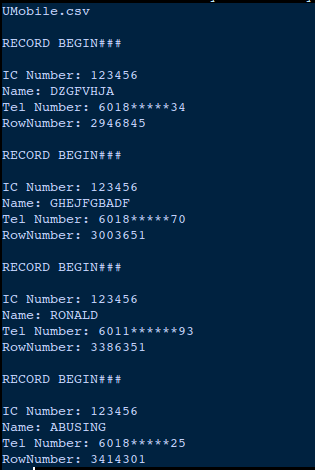
Upon further analyzing the data, I went back to the original source files and notice something strange, the account numbers belonged to some strange names. And then it made sense — this was Test data.

Test data in a Production Environment to be exact.

And when the Database for the telco was dumped, the telco’s didn’t remove these test accounts from their system. So what we have is a bunch of dummy accounts, with dummy IC numbers.

What is Test data in Production?

Let’s take a step back.

In IT projects, production is simply the name we give the servers that are actually producing something for the company. It’s the servers that run the day-to-day activity.

The opposite of Production is test. Test servers, are servers were developers test their code and have fund around with. Test servers are purely for testing code, before they hit Production. P

What you want to avoid is a situation where developers are pushing un-tested code into Production — that can really screw things up.

However, sometimes, things need to be tested in Production as well. i.e. Testing in a real-live environment.

Now imagine you’re a large telco, and you want to roll out a new postpaid plan. First you configure that plan on a test environment, then you run some test to figure out if it works, and finally to deploy that code to production. Very simplistic analogy, but it works.

Sometimes you want to test how your code is doing in Production as well. So you create some dummy accounts in Production, and test out new functionality using these dummy accounts. You might make calls withe the dummy accounts, and see if the billing matches up to what you configured.

That’s the only way you can be sure, that your new postpaid plan is working as promised. Those dummy accounts might be just for testing — but they exist on a production server.

So if you downloaded the production database of a large telco — chances are you’d find a whole load of dummy accounts for this specific purpose. And hence why IC Number 123456 exist across multiple telcos.

To be honest, now that I realize this, it would have been odd if these accounts didn’t exist.

So you’re not a phishing site

No. A large number of folks have already reported that the data on the site is accurate. So it’s clear I have the data.

Why would I phish for something I already have?

Plus to assure you further, I keep no logs of what hits the API. I do have Google Analytics on page, for me to keep track of how many users are on it — but that’s it, nothing else.

Conclusion

You might not trust me, and that’s fine. After all, I’m from Klang.

And honestly, typing your IC number into a dodgy website named sayakenahack isn’t the best idea in the world. But disclosures like this are a infosec norm these days, and unfortunately if you want to see if your personal data was stolen, you have to give some of it to the person who’s checking.

If you want to find out if your IC is in the system — you have to give me your IC number. There’s no alternative.

So what we need a trustworthy 3rd-party that can provide this data to you. I’ve kept this blog for 6 years now, and I think I’ve built up a good enough reputation to be such a party.

This blog has no adverts, and neither does sayakenahack. I could easily make money from the ~50k visitors who’ve already visited the site, but I choose not to. My reputation is worth more than the money that shitty adverts could ever bring in.

So after spending more than 40 hours coding, and about $30 in AWS charges, I make no money in return.

This blog runs at a nett loss every year :), but that’s OK. Because Malaysians need someone to report on tech issues properly.

I code for fun (not profit), and I definitely don’t phish.

TL;DR