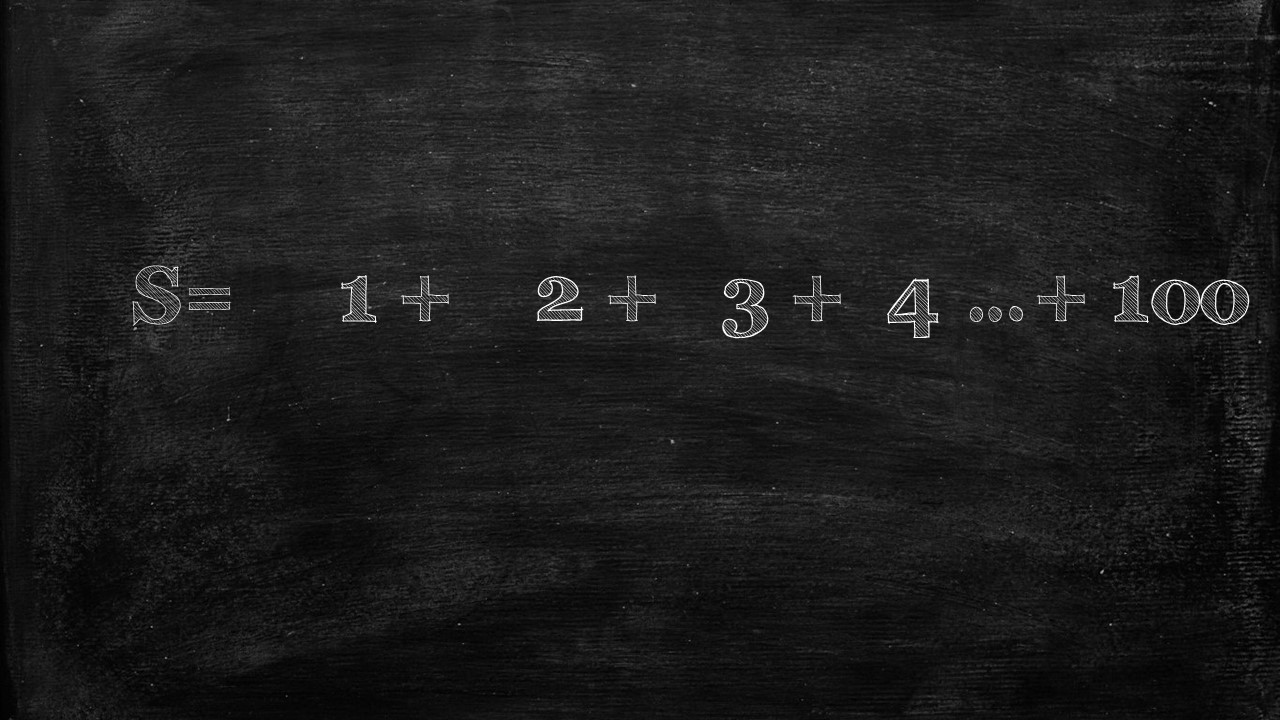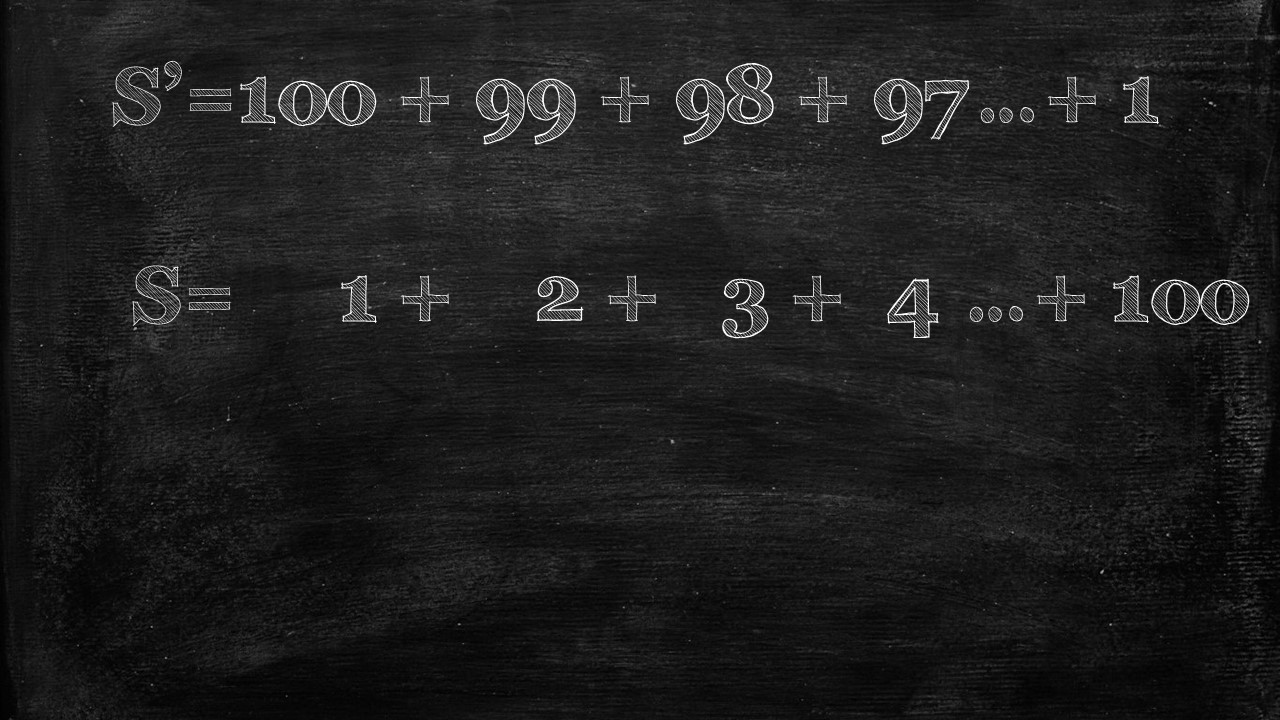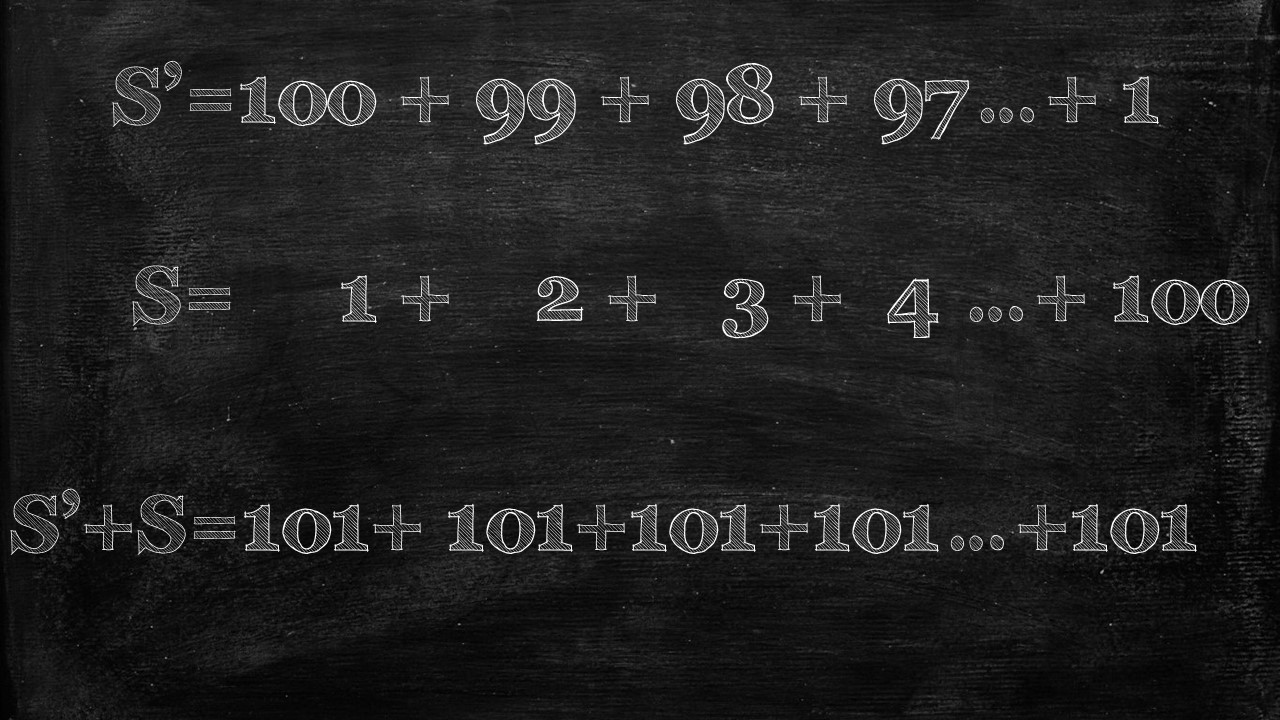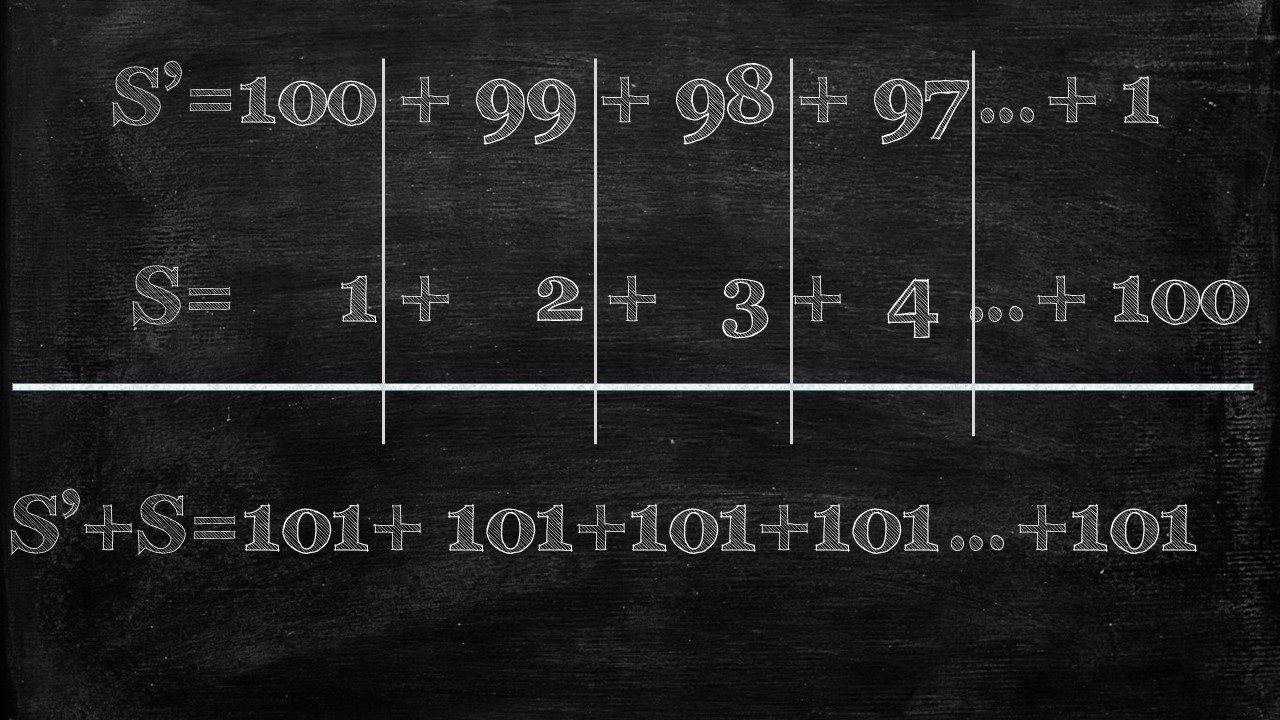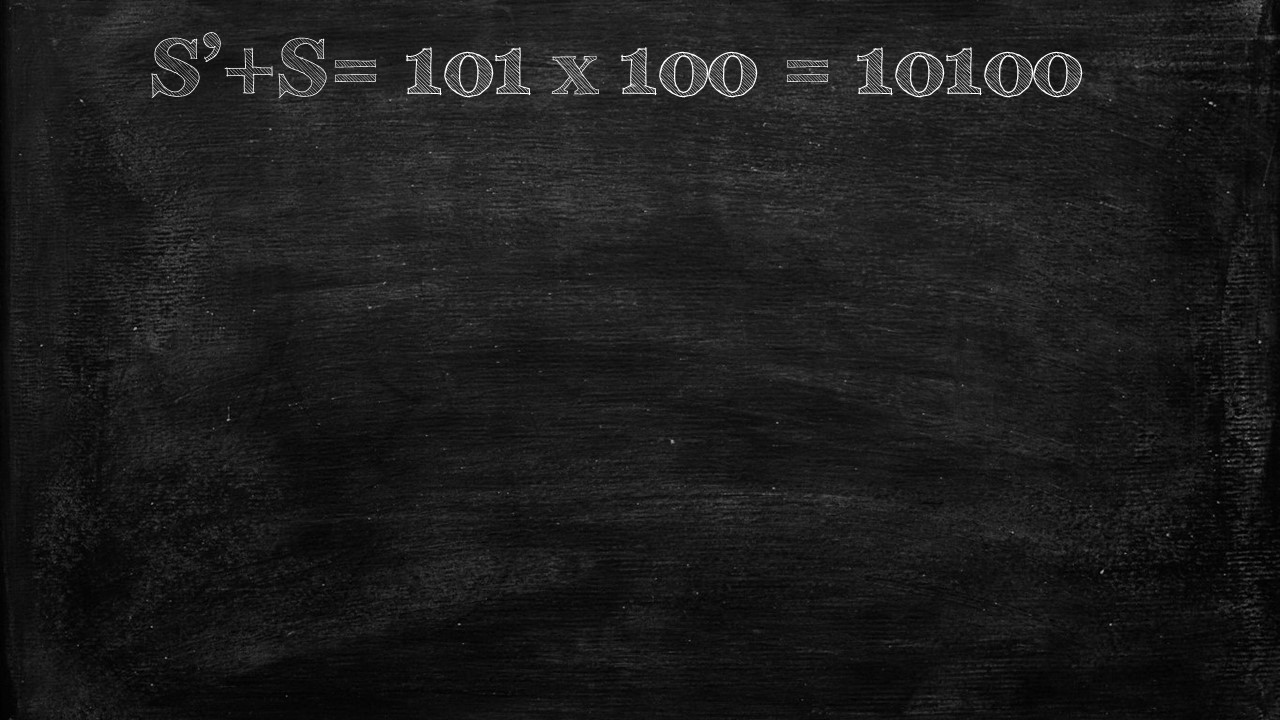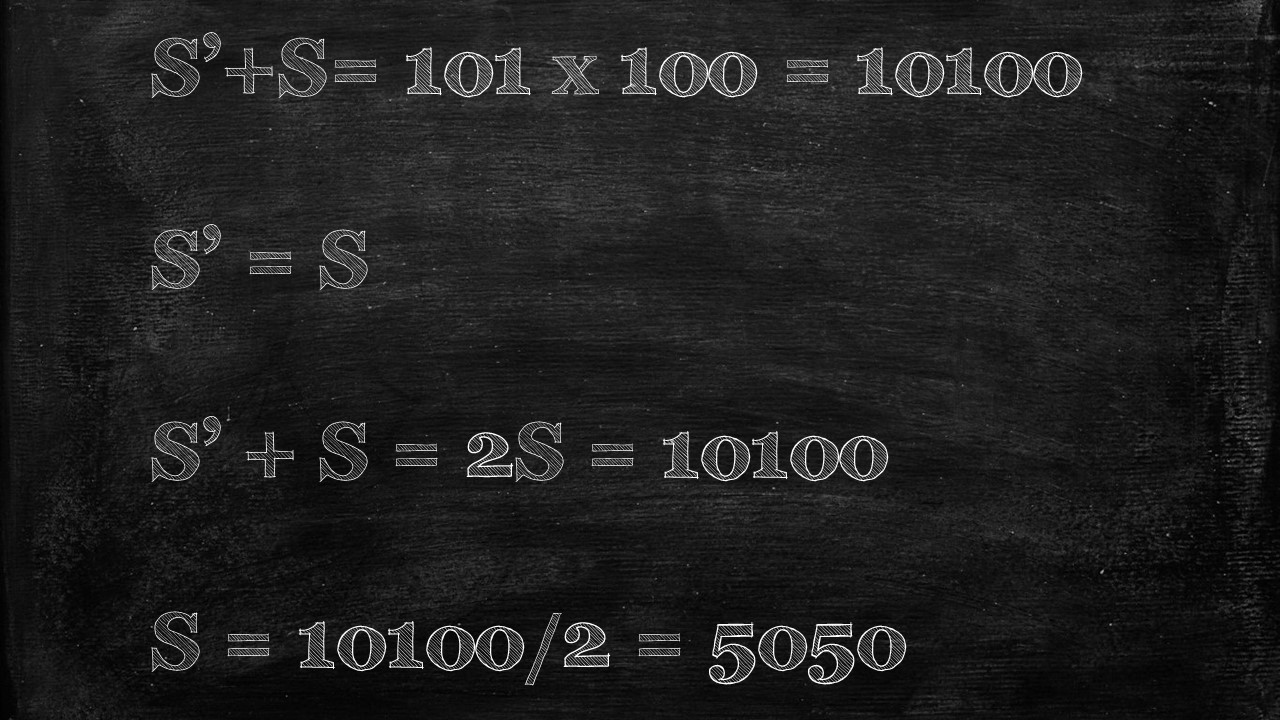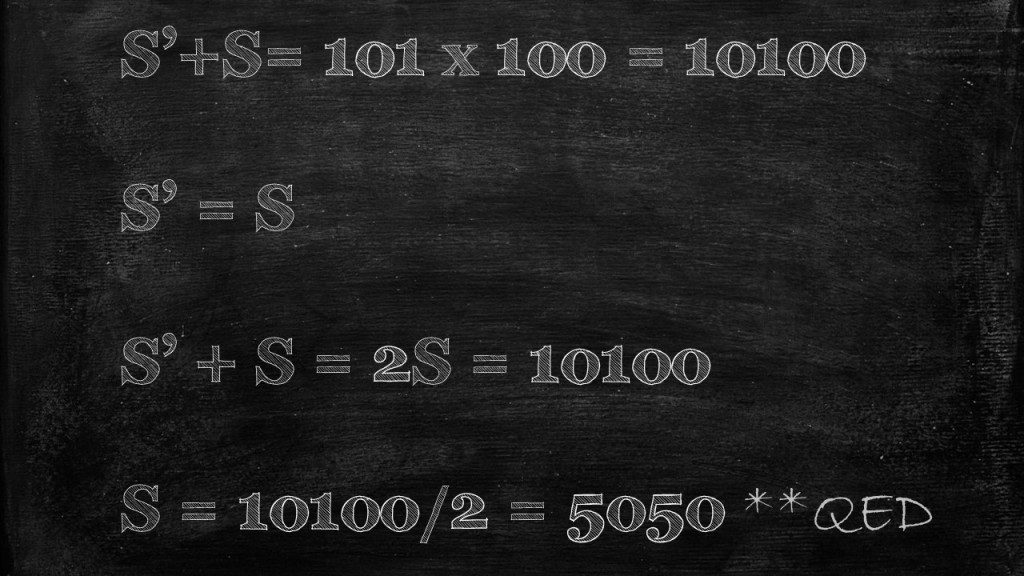Teachers day was last Friday, and I thought it would be good to make a small post in tribute to an interesting teacher I had in form 4.
Imagine a 200 pound man, with a thick moustache, carrying intimidating rotan, and wore nothing but Chairman Mao style Bush-coats everyday–that’s Mr. Vijay, and he thought me Additional Mathematics.
Mr. Vijay was interesting in many ways, including the wrestling stories he’d tell in class, but for all my years in school I only remember a handful of lessons, and none more vividly than the time he thought me the story of Carl Friedrich Gauss during us lesson on arithmetic sequences.
The story is certainly fiction, similar to that of Newton discovering gravity by watching an apple fall from a tree–but that is irrelevant, what’s relevant is how I remember it, and as my tribute to one of my teachers, I’d re-tell the story here.
Here goes.
Once upon a time, there lived a boy named Carl Friedrich Gauss.
Even while still in elementary school, Carl was already a maths genius, and like all other geniuses was a bit of a nuisance in class. So one day to shut Carl up, his teacher gave him an ‘important assignment’–he was to calculate the sum of all numbers from 1 to 100. i.e. 1+ 2+ +3 +4….+100. The idea was that this would keep Carl busy for the remainder of the lesson
However, Carl came back very quickly with an answer of 5,050!!
How did Carl do this?!!
First Carl said, we’ll assume the answer to our Sum is S–and S is the 1+2+3+4…100.
But Carl added, let’s also create the same calculation, but counting backwards, 100+ 99+ 98 +97….+1. Which Carl called S’ (or called S prime)
If we then add S + S’, but do so in special way. We take the first number in S (1), and add it to the first number in S’ (100). Then we take the second number in S (2) and add it to the second number in S’ (99), and do so for all the 100 numbers in both series.
What we end up with is a series of 101 repeated 100 times.
Let’s draw some lines so you can see a bit clearer.
Now it’s quite easy to sum up S’ + S, which is simply 101 x 100.
Since S’ and S are the same series (just reversed), S’ +S = 2S, and now we can find S.
And since S is what we denoted as the sum of all numbers 1 to 100, well then the answer has to be 5050.
Of course, anyone who knew Mr. Vijay would know it wouldn’t end it there. He would denote the entire thing as QED which is short for ‘quite easily done’, and capped off the story by saying “If Carl Friedrich Gauss in the 1700’s can solve this while in elementary school–no reason why none of you can’t do it”.
The beautiful thing is that while this story was told to me more then 15 years ago…I remember it to this day. When a solution is this elegant you can’t help but be amazed, and I think that amazement etched this into my memory cells.
And they say Add Maths is hard!!
I tried Googling Mr. Vijay, but couldn’t find anything, but here’s to Mr. Vijay wherever he may be.